Dijkstra算法求最短生成路径

简介

最短路径：在网图中，两顶点之间经历的边上权值之和最少的路径。
Dijkstra算法：迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

基本思想：
1.初始化数组dist,path和s
2.while(s中的元素个数<n)

在dist[n]中求最小值，其编号为k；
输出dist[k]和path[k]
修改数组dist和path
将顶点k添加至数组s

该有向图如下：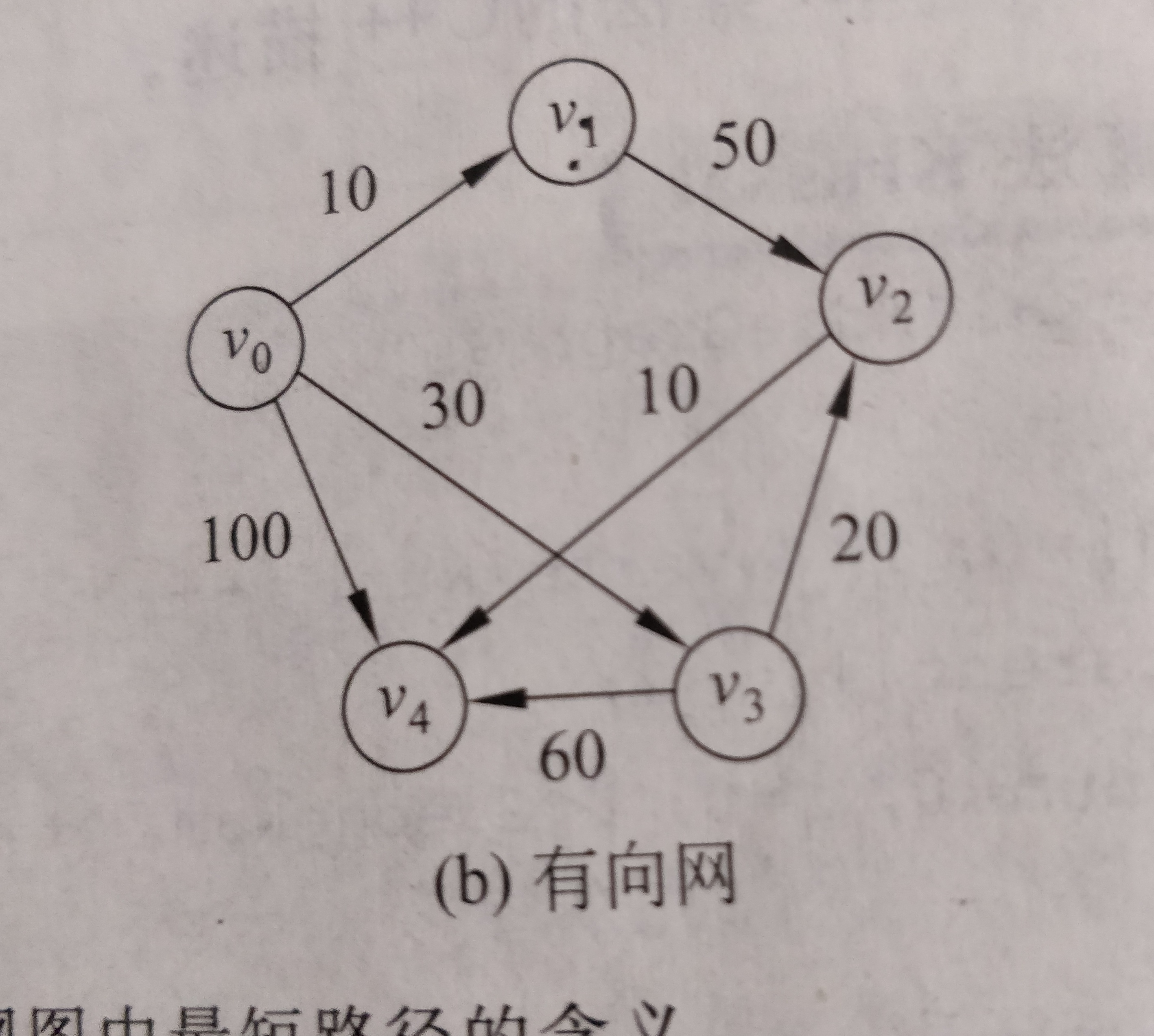

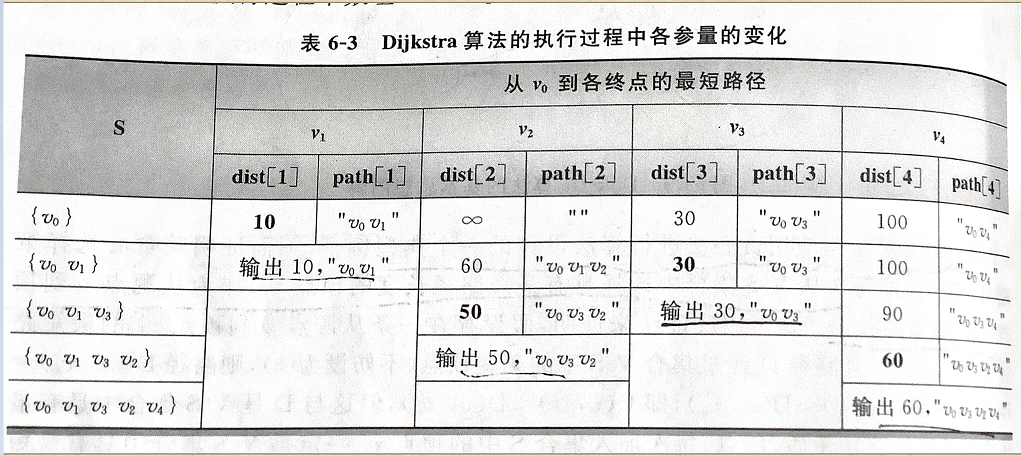
求最短生成路径各分量的变化

TIM截图20191214143115.png

代码实现

此处我采用邻接矩阵储存该有向图，为了省时间（其实是自己懒），此处省略邻接矩阵的构造过程，采用手动写入边集构建该有向图。

MGraph类

package Dijkstra;

/**
 * @Author {zbl}
 * @Date: 2019/12/14/ 13:04
 * @Description
 */
public class MGragh {
    public static final int   INT_MAX= 0x7ffffff;

    //邻接矩阵，边集
    public int[][] arc = {
            {INT_MAX,10,INT_MAX,30,100},
            {INT_MAX,INT_MAX,50,INT_MAX,INT_MAX},
            {INT_MAX,INT_MAX,INT_MAX,INT_MAX,10},
            {INT_MAX,INT_MAX,20,INT_MAX,60},
            {INT_MAX,INT_MAX,INT_MAX,INT_MAX,INT_MAX}
    };
    //顶点数
    public int vertexNum = 5;
    //空构造方法
    public MGragh(){}
}

主函数：

package Dijkstra;

import java.nio.file.attribute.DosFileAttributes;
import java.util.ArrayList;
import java.util.List;

/**
 * @Author {zbl}
 * @Date: 2019/12/14/ 13:02
 * @Description
 */
public class Main {
    /**
    * @Description: 主函数
    * @Param: [args]
    * @return: void
    * @Author: {zbl}
    * @Date: 2019/12/14
    */
    
    public static void main(String[] args){
        MGragh g = new MGragh();
        Dijkstra(g,0);
    }

    /**
    * @Description: Dijkstra算法
    * @Param: [mGragh, n]
    * @return: void
    * @Author: {zbl}
    * @Date: 2019/12/14
    */
    
    public static void Dijkstra(MGragh mGragh,int n){
        //加入的顶点集
        List<Integer> v = new ArrayList<>();
        //路径
        String[] path = new String[mGragh.vertexNum];
        //边集权值
        int[] dist = new int[mGragh.vertexNum];
        //初始化dist,path
        for (int i = 0; i<mGragh.vertexNum; ++i){
            dist[i] = mGragh.arc[n][i];
            if(dist[i]!=MGragh.INT_MAX) path[i] = "V"+n+"V"+i;
            else path[i] = "";
        }
        v.add(n);
        //点集中元素个数少于顶点数
        while(v.size()<mGragh.vertexNum){
            int k,i;
            //找到dist中最小的
            for (k=0,i = 1; i<mGragh.vertexNum; ++i){
                if(dist[i]!=0 && dist[i]<dist[k]) k=i;
            }
            //输出dist和path
            System.out.println(dist[k]+"  "+path[k]);
            v.add(k);
            //更新dist和path数组
            for (i = 0; i<mGragh.vertexNum; ++i){
                if(dist[i]>dist[k] + mGragh.arc[k][i]){
                    dist[i] = dist[k] + mGragh.arc[k][i];
                    path[i] = path[k] + "V" + i;
                }
            }
            dist[k] = 0;
        }
    }
}