Prim算法求最小生成树

简介

最小生成树：一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边（边的代价和最小）

Prim算法是求最小生成树的一种方法，由于Prim算法的复杂度与边的数量无关，于是较适用于求稠密网的最小生成树。

Prim算法的基本思想是：
1、初始化：U={v0}； TE={}；
2、重复下述操作直到U=V：

2.1 在E中寻找最短边（u，v），且满足u∈U，v∈V；
2.2 U=U+{v}；
2.3 TE=TE+{ (u，v) }；

求最小生成树的步骤

无向图如下图所示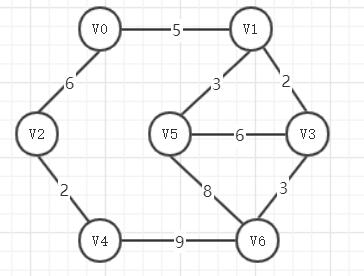

Prim算法求最小生成树的步骤：

代码实现

此处我采用邻接矩阵储存该无向图，为了省时间（其实是自己懒），此处省略邻接矩阵的构造过程，采用手动写入边集和点集构建该无向图。

Prim算法代码实现：

     /**
     * Prim算法
     * @param G 无向图
     * @param shortEdge 辅助边集
     */
    public static void Prim(MGraph G, ShortEdge[] shortEdge){
        //初始化辅助数组
        for (int i = 0;i<G.vertexNum;++i){
            shortEdge[i].lowcast = G.arc[0][i];
            shortEdge[i].adjvex = i;
        }
        //将顶点0加入集合U
        shortEdge[0].lowcast = 0;
        //建立辅助顶点集合
        int[] verctor = new int[G.vertexNum];
        verctor[0]++;
        for (int i = 1;i<G.vertexNum;++i){
            //寻找最短边的邻接点k
            int k = MinEdge(shortEdge,G.vertexNum);
            //打印
            System.out.println("(顶点：" + k + ",边的权值：" + shortEdge[k].lowcast + ")");
            //将顶点k加入集合U
            shortEdge[k].lowcast = 0;
            verctor[k]++;
            for (int j = 0;j<G.vertexNum;++j){
                //若该点已加入集合U,则跳过该点
                if(verctor[j]>0) continue;
                //更新辅助数组,选取最新的邻接边更新至辅助数组
                if ((G.arc[k][j]<shortEdge[j].lowcast || shortEdge[j].lowcast==0 )&& G.arc[k][j]!=0){
                    shortEdge[j].lowcast = G.arc[k][j];
                    shortEdge[j].adjvex = j;
                }
            }
        }
    }

完整代码
无向图存储类MGraph

package Prim;

/**
 * @Author zbl
 * @Date: 2019/11/21/ 10:52
 * @Description
 */
public class MGraph {
    //边集
    public int[][] arc ={
            {0,5,6,0,0,0,0},
            {5,0,0,2,0,3,0},
            {6,0,0,0,2,0,0},
            {0,2,0,0,0,6,3},
            {0,0,2,0,0,0,9},
            {0,3,0,6,0,0,8},
            {0,0,0,3,9,8,0}
    };

    //顶点数
    public int vertexNum = 7;
    //空构造函数
    public MGraph(){};

}

储存最短边的辅助类：

package Prim;

/**
 * @Author zbl
 * @Date: 2019/11/21/ 11:04
 * @Description
 */
public class ShortEdge {
    //权值
    public int lowcast;
    //邻接点
    public int adjvex;
}

主要代码：

package Prim;

/**
 * @Author zbl
 * @Date: 2019/11/21/ 10:50
 * @Description
 */

public class Main {
    //主函数
    public static void main(String[] args) {
        //建立辅助数组
        ShortEdge[] shortEdges = new ShortEdge[7];
        for(int i = 0;i<7;++i){
            shortEdges[i] = new ShortEdge();
        }
        Prim(new MGraph(),shortEdges);
    }

    /**
     * Prim算法
     * @param G 无向图
     * @param shortEdge 辅助边集
     */
    public static void Prim(MGraph G, ShortEdge[] shortEdge){
        //初始化辅助数组
        for (int i = 0;i<G.vertexNum;++i){
            shortEdge[i].lowcast = G.arc[0][i];
            shortEdge[i].adjvex = i;
        }
        //将顶点0加入集合U
        shortEdge[0].lowcast = 0;
        //建立辅助顶点集合
        int[] verctor = new int[G.vertexNum];
        verctor[0]++;
        for (int i = 1;i<G.vertexNum;++i){
            //寻找最短边的邻接点k
            int k = MinEdge(shortEdge,G.vertexNum);
            //打印
            System.out.println("(顶点：" + k + ",边的权值：" + shortEdge[k].lowcast + ")");
            //将顶点k加入集合U
            shortEdge[k].lowcast = 0;
            verctor[k]++;
            for (int j = 0;j<G.vertexNum;++j){
                //若该点已加入集合U,则跳过该点
                if(verctor[j]>0) continue;
                //更新辅助数组,选取最新的邻接边更新至辅助数组
                if ((G.arc[k][j]<shortEdge[j].lowcast || shortEdge[j].lowcast==0 )&& G.arc[k][j]!=0){
                    shortEdge[j].lowcast = G.arc[k][j];
                    shortEdge[j].adjvex = j;
                }
            }
        }
    }

    /**
     * 获取最小邻接点
     * @param shortEdges 辅助边集
     * @param num 图的顶点数目
     * @return 最小邻接点
     */
    public static int MinEdge(ShortEdge[] shortEdges,int num){
        int min = 999999999;
        int result = 0;
        //遍历获取与集合U中都点权值最小的邻接点及其该最小边
        for (int i = 0;i<num;++i){
            if (min > shortEdges[i].lowcast && shortEdges[i].lowcast!=0){
                min = shortEdges[i].lowcast;
                result = shortEdges[i].adjvex;
            }
        }
        return result;
    }
}

运行结果：