# Kruskal算法求最小生成树 ## 简介 上一篇博客介绍了用Prim算法求无向图的最小生成树,Prim算法适合用求稠密网的最小生成树,那么当网内的边较少时Prim算法显然就不适用了,于是Kruskal算法便随之诞生了。 **Kruskal算法**是求最小生成树的一种方法,适用于求稀疏网的最小生成树。 Kruskal算法的`基本思想`是: 1、初始化:U=V; TE={}; 2、重复下述操作直到T中的连通分量个数为1: * 2.1 在E中寻找最短边(u,v),且满足u∈U,v∈V; * 2.2 如果顶点u,v位于T的两个不同连通分量,则 2.2.1 将边(u,v)并入TE; 2.2.2 将这两个连通分量合为一个; * 2.3 在E中标记边(u,v),使得(u,v)不参加后续最短边的选取 显然,实现Kruskal算法的`关键之处`在于:如何叛变被考察边的两个顶点是否位于`两个`连通分量(即是否与生成树中的 边形成回路) ## 求最小生成树的步骤 无向图如下图所示 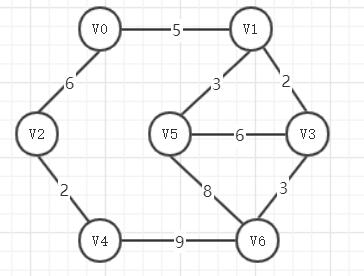 Kruskal算法求最小生成树的步骤: 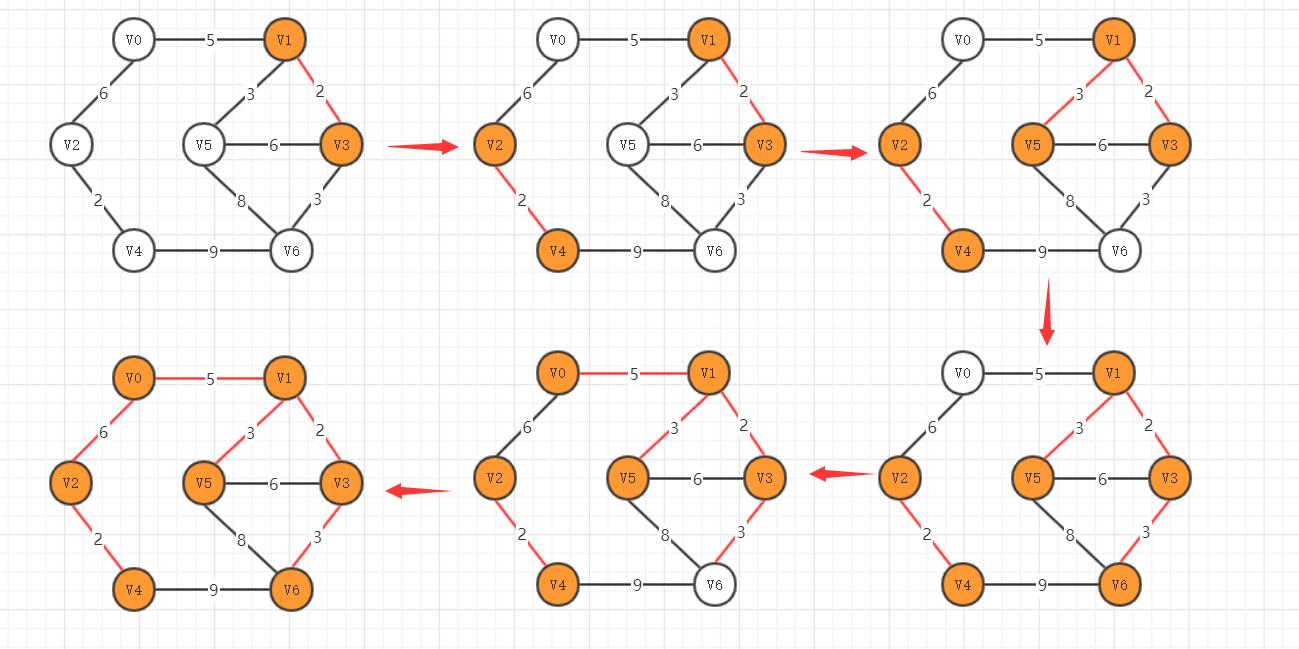 ## 代码实现 此处我采用邻接矩阵储存该无向图,边集储存该图中的边,为了省时间(其实是自己懒 ),此处省略邻接矩阵的构造过程,采用手动构建该无向图,通过无向图构建边集。 `Kruskal算法代码实现`: ```java /** * Kruskal算法 * @param G */ public static void Kruskal(EdgeGraph G){ int[] parent = new int[G.vertexNum]; //初始化parent数组 for (int i = 0; i<G.vertexNum;++i){ parent[i] = -1; } for (int num = 0,i = 0; i<G.edgeNum; ++i){ int vex1 = FindRoot(parent,G.edge[i].from); int vex2 = FindRoot(parent,G.edge[i].to); if(vex1 != vex2){ //输出加入的边 System.out.println("(" + G.edge[i].from + "," + G.edge[i].to + "),weight:" + G.edge[i].weight); //合并生成树 parent[vex2] = vex1; ++num; if (num == G.vertexNum-1) return; } } } ``` **完整代码** 无向图存储类EdgeGraph ```java package Kruskal; /** * @Author zbl * @Date: 2019/11/23/ 17:33 * @Description */ public class EdgeGraph { int[] vertex = new int[7]; Edge[] edge = new Edge[9]; int vertexNum = 7; int edgeNum = 9; public EdgeGraph(){ //此处省略构造过程 for (int i = 0; i<vertexNum;++i) vertex[i] = i; int[][] arc ={ {0,5,6,0,0,0,0}, {5,0,0,2,0,3,0}, {6,0,0,0,2,0,0}, {0,2,0,0,0,6,3}, {0,0,2,0,0,0,9}, {0,3,0,6,0,0,8}, {0,0,0,3,9,8,0} }; int count = 0; for (int i = 0;i<7; ++i){ for (int j = i; j<7; ++j){ if(arc[i][j]!=0){ edge[count] = new Edge(); edge[count].from = i; edge[count].to = j; edge[count++].weight = arc[i][j]; } } } //记录最后一次交换的位置 int lastExchangeIndex = 0; //无序数列的边界,每次只需比较到这里为止 int sortBorder = edge.length - 1; for (int i = 0;i<edge.length - 1;++i){ boolean flag = true; for (int j = 0;j<sortBorder;++j){ if(edge[j].weight > edge[j+1].weight){ Edge tmp = edge[j]; edge[j] = edge[j+1]; edge[j+1] = tmp; //更新最后一次交换的位置 lastExchangeIndex = j; flag = false; } } //更新边界 sortBorder = lastExchangeIndex; if(flag) break; } } } ``` 储存边的辅助类: ```java package Kruskal; /** * @Author zbl * @Date: 2019/11/23/ 17:34 * @Description */ public class Edge { int from; int to; int weight; } ``` --- 主要代码: ```java package Kruskal; /** * @Author zbl * @Date: 2019/11/23/ 16:38 * @Description */ public class Main { /** * Kruskal算法 * @param G */ public static void Kruskal(EdgeGraph G){ int[] parent = new int[G.vertexNum]; //初始化parent数组 for (int i = 0; i<G.vertexNum;++i){ parent[i] = -1; } for (int num = 0,i = 0; i<G.edgeNum; ++i){ int vex1 = FindRoot(parent,G.edge[i].from); int vex2 = FindRoot(parent,G.edge[i].to); if(vex1 != vex2){ //输出加入的边 System.out.println("(" + G.edge[i].from + "," + G.edge[i].to + "),weight:" + G.edge[i].weight); //合并生成树 parent[vex2] = vex1; ++num; if (num == G.vertexNum-1) return; } } } public static int FindRoot(int[] parent,int v){ int t = v; //求顶点t的双亲 if(parent[t] > -1) t = parent[t]; return t; } public static void main(String[] args){ Kruskal(new EdgeGraph()); } } ``` 运行结果: 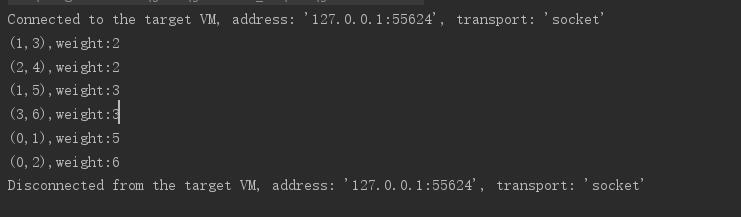 ## 复杂度 分析Kruskal算法,设连通网中有n个顶点e条边,则第一个进行初始化的循环语句需要执行n次,第二个循环最多执行e次,最少执行n-1次,函数FindRoot的循环语句最多执行log2n次,由于在执行Kruskal算法之前需要对边集数组进行排序,此处采用冒泡排序O(n²)`(采用快排需要O(elog2e))`,所以,此处Kruskal算法的时间复杂度为O(n²),`但实际可优化为O(elog2e)`。 ## 参考文献 * 王红梅,胡明,王涛编著. 数据结构(C++版)(第二版)[M]. 清华大学出版社. 最后修改:2020 年 02 月 27 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏
2 条评论
文章结构紧凑,层次分明,逻辑严密,让人一读即懂。
你的文章内容非常精彩,让人回味无穷。http://www.hzrsdt.com